Barisan dan Deret Geometri serta Deret Geometri Tak Hingga ~ Selamat Datang di Kennycandra Blog!!

Assalamu'alaikum, Hai gengs. jika kamu sudah membaca postingan sebelumnya tentang baris dan deret Aritmatika (baca lagi: Barisan Aritmatika) di dalamnya sudah dibahas mengenai definisi dari barisan dan deret. Nah, Selain baris dan deret Aritmatika, ada satu lagi loh yang bakal kita bahas kali ini, yaitu baris dan deret Geometri. Apasih baris dan deret Geometri itu ? apa perbedaannya dengan baris dan deret Aritmatika ? langsung aja scroll ke bawah supaya gak bingung ! Check this out !

Daftar Isi :

Barisan Geometri
Deret Geometri
Deret Geometri Tak hingga

Baris Geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan r. yang mana r adalah pembanding dua suku berurutan yang selalu bernilai tetap/sama. pembanding dari dua suku berurutan tersebut disebut dengan rasio, ditulis r.

Adapun rumus umum untuk rasio pada Geometri, yaitu :

$r=\frac{U_n}{U_{n-1}}$

Misalnya 1,2,4,8,16,.... merupakan baris Geometri dengan nilai

$\frac{16}{8}=\frac{8}{4}=\frac{4}{2}=\frac{2}{1}=2 (konstan)$

Nah, kalau kamu sudah mengetahui nilai a dan r, maka sekarang kita pelajari rumus suku ke-n.

Rumus suku ke-n

$U_n=ar^{n-1}$

Keterangan :
$U_n$ : suku ke-n
a : suku pertama
r : rasio
n : banyak suku

Suku tengah barisan Geometri
Jika suatu barisan Geometri memiliki jumlah suku ganjil, maka barisan tersebut memiliki suku tengah. Suku tengah suatu barisan Geometri adalah $U_{\frac{1}{2}(n+1)}$ . jika diselesaikan dengan rumus $U_n=ar^{n-1}$ akan menjadi :
$U_n=ar^{n-1}$
$U_{\frac{1}{2}(n+1)}=ar^{\frac{1}{2}(n+1)-1}$
$U_{\frac{1}{2}(n+1)}=ar^{\frac{1}{2}n-\frac{1}{2}}$
$U_{\frac{1}{2}(n+1)}=ar^{\frac{1}{2}(n-1)}$
$U_{\frac{1}{2}(n+1)}=a\sqrt[2]{r^{n-1}}$
$U_{\frac{1}{2}(n+1)}=\sqrt[2]{a^2r^{n-1}}$
$U_{\frac{1}{2}(n+1)}=\sqrt[2]{aar^{n-1}}$
$U_{\frac{1}{2}(n+1)}=\sqrt[2]{a\times U_n}$

Sisipan Pada Barisan Geometri

Jika antara dua suku barisan geometri disisipkan k buah suku sehingga membentuk barisan Geometri baru maka rasio dari barisan Geometri pun akan berubah. Rasio dari barisan Geometri yang sudah disisipkan k buah suku sebagai berikut.

$r'=\sqrt[k+1]{r}$

Keterangan :
$r'$ = rasio barisan Geometri yang telah disisipkan k buah suku

k = banyak suku yang disisipkan

Banyak suku dari barisan Geometri yang disisipkan k buah suku juga akan berubah, menjadi sebagai berikut :

$n'=n+(n-1)k$

Keterangan :

$n'$ = banyak suku barisan geometri yang baru

k = banyak suku barisan geometri mula-mula

Deret Geometri adalah penjumlahan dari suku-suku dari suatu barisan Geometri. Penjumlahan dari suku pertama sama suku ke-n barisan Geometri dinotasikan 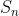$S_n$ dan memiliki rumus sebagai berikut.

$S_n=U_1+U_2+U_3+...+U_{n-1}+U_n$

atau sebagai :

$S_n=a+ar+ar^2+ar^3+...+ar^{n-2}+ar^{n-1}$

Jika hanya diketahui nilai a adalah suku pertama dan nilai 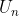$U_n$ adalah suku ke-n, maka rumus deret Geometrinya adalah :

$S_n=\frac{a(r^n-1)}{r-1}$ , dengan syarat r > 1

$S_n=\frac{a(1-r^n)}{1-r}$ , dengan syarat r < 1

Suatu deret Geometri dapat menjumlahkan suku-sukunya sampai menuju tak hingga. Apabila deret Geometri menuju tak hingga dimana 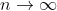$n \to \infty$ , maka deret ini dapat ditulis sebagai berikut.

$S_n=U_1+U_2+U_3+U_4+...$ atau $S_n=a+ar+ar^2+ar^3+...$

Deret Geometri Tak hingga terbagi menjadi dua Jenis, yaitu Konvergen dan Divergen.

Deret Geometri Tak hingga bersifat Konvergen ketika penjumlahan dari suku-sukunya mendekati suatu bilangan tertentu.
Deret Geometri Tak hingga bersifat Divergen ketika penjumlahan dari suku-sukunya tidak terbatas

Nilai Deret Geometri tak hingga dapat ditentukan dengan menggunakan limit. sebelumnya kita ketahui bahwa rumus umum deret Geometri adalah :

$S_n=\frac{a(1-r^n)}{1-r}$

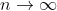Dimana terdapat unsur $r^n$ di dalam perhitungannya yang terpengaruh jumlah suku n. Jika $n \to \infty$ , maka untuk menentukan $r^n$ dapat menggunakan limit, yaitu :

$lim_{n \to \infty}r^n=0$ , dengan syarat $-1<r<1$

$lim_{n \to \infty }r^2=\infty$ dengan syarat $r<-1 \ atau \ r>1$

Kemudian hasil limit $r^n$ tersebut dimasukkan ke dalam perhitungan deret menjadi :
$S_\infty =\frac{a(1-lim_{n \to \infty}r^n)}{1-r}=\frac{a(1-0)}{1-r}=\frac{a}{1-r}$
dengan syarat $-1<r<1$

$S_\infty =\frac{a(1-lim_{n \to \infty}r^n)}{1-r}=\frac{a(1-\infty )}{1-r}=\infty$

dengan syarat $r<-1 \ atau \ r>1$

Sehingga, barisan Geometri yang memiliki rasio antara -1 sampai 1 disebut dengan barisan Geometri yang Konvergen. Deret Geometri dari suatu barisan Geometri yang Konvergen dan banyak suku tak hingga dapat dihitung dengan rumus sebagai berikut :

$S_\infty =\frac{a}{1-r}$

Keterangan :

a = suku pertama

k = rasio dengan syarat $r<-1 \ atau \ r>1$

-----------------------------------------------------------------------------------------------------------------------------------------

Mungkin itu saja pembahasan kali ini tentang Notasi Sigma yang bisa saya jabarkan, semoga saja pembahasan ini berguna bagi teman-teman semua, terutama teman-teman jenjang Sekolah Menengah Atas. Terima kasih sudah mengunjungi kennycandra Blog. Nantikan postingan berikutnya ya !

Minggu, 22 Maret 2020

Barisan dan Deret Geometri serta Deret Geometri Tak Hingga

0 komentar:

Tentang Saya

Popular Posts

Recent Posts

Categories

Pages

Blog Archive

Visitors

Formulir Kontak