Assalamu'alaikum, Hai gengs. Pada pertemuan kali ini Kennycandra Blog akan membahas tentang baris dan deret Aritmatika. yang mana konsep Baris dan Deret ini banyak teman-teman temui di kehidupan sehari-hari. Nah, sekarang kita akan sama-sama tahu apa pentingnya memahami materi ini. Yuk Scroll ke bawah untuk penjelasan lebih lengkapnya !
Daftar Isi :
- Pengertian Baris dan Deret
- Barisan Aritmatika
- Deret Aritmatika
- Sisipan pada Barisan Aritmatika
- Suku Tengah Barisan Aritmatika
Barisan Merupakan urutan dari suatu anggota-anggota himpunan berdasarkan suatu aturan atau karakteristik tertentu. setiap anggota himpunan diurutkan berdasarkan urutan/suku pertama, kedua, ketiga, dan seterusnya. untuk menyatakan urutan/ suku ke-n dari suatu barisan dinotasikan
Contoh Barisan :
- 1, 2, 3, 4, 5, 6, ...
- 2, 4, 6, 8, 10, ...
- 1, 3, 5, 7, 9, 11, ...
Sedangkan Deret merupakan penjumlahan dari suku-suku suatu barisan. Penjumlahan suku-suku tersebut dapat juga dinyatakan dalam Notasi Sigma (Baca Juga: Notasi Sigma). Barisan dari suku  yang dinyatakan dalam fungsi
yang dinyatakan dalam fungsi =U_{n}) memiliki deret sebagai berikut :
memiliki deret sebagai berikut :


Suatu barisan  disebut barisaan aritmatika jika selisih antar dua suku yang berurutan selalu tetap. selisih tersebut disebut "beda" dan dilambangkan dengan b. sehingga :
disebut barisaan aritmatika jika selisih antar dua suku yang berurutan selalu tetap. selisih tersebut disebut "beda" dan dilambangkan dengan b. sehingga :

Sebagai contoh, 2, 4, 6, 8,... merupakan baris aritmatika dengan nilai b :
b = 8 - 6 = 6 - 4 = 4 - 2 = 2
Jika suku pertama dinyatakan dengan a, maka bentuk umum barisan aritmatika adalah :

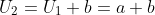
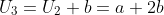

...
b)
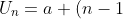b) ; dimana n bilangan asli
; dimana n bilangan asli
bentuk di atas adalah bentuk umum dari barisan aritmatika
sehingga,
Untuk mengetahui nilai suku ke-n dari suatu barisan aritmatika dapat diketahui dengan mengetahui nilai suku pertama dan selisih antar suku yang berdekatan (b).

Deret Aritmatika adalah penjumlahan dari suku-suku anggota barisan aritmatika. Jumlah n suku pertama deret aritmatika disimbolkan dengan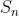 . Penjumlahan dari semua anggota barisan ini dapat dihitung sebagai :
. Penjumlahan dari semua anggota barisan ini dapat dihitung sebagai :
+(a+2b)+...+(a+(n-1)b))
atau sebagai :
b)))





 = beda barisan aritmatika yang telah disisipkan k buah suku
= beda barisan aritmatika yang telah disisipkan k buah suku
 = banyak jumlah suku yang disisipkan
= banyak jumlah suku yang disisipkan
k)
 = banyak suku barisan aritmatika baru
= banyak suku barisan aritmatika baru
 = banyak suku barisan aritmatika lama
= banyak suku barisan aritmatika lama
) Jika barisan aritmatika memiliki jumlah suku ganjil, maka memiliki suku tengah. Suku tengah suatu barisan aritmatika adalah :
Jika barisan aritmatika memiliki jumlah suku ganjil, maka memiliki suku tengah. Suku tengah suatu barisan aritmatika adalah : }) . Jika diselesaikan dalam rumus
. Jika diselesaikan dalam rumus 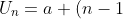b) , maka nilai suku tengah didapat :
, maka nilai suku tengah didapat :
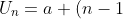b)
}=a+(\frac{1}{2}(n+1)-1)b)
}=a+(\frac{1}{2}n-\frac{1}{2})b)
}=a+\frac{1}{2}(n-1)b)
}=\frac{2a+(n-1)b}{2})
}=\frac{a+a+(n-1)b}{2})
}=\frac{a+U_n}{2})
-------------------------------------------------------------------------------------------------------------------------------------------
Mungkin itu saja pembahasan kali ini tentang Baris dan Deret Aritmatika yang bisa saya jabarkan, semoga saja pembahasan ini berguna bagi teman-teman semua, terutama teman-teman pada jenjang Sekolah Menengah Atas. Terima kasih sudah mengunjungi kennycandra Blog. Baca Juga : Barisan dan Deret Geometri
Sebagai contoh, 2, 4, 6, 8,... merupakan baris aritmatika dengan nilai b :
b = 8 - 6 = 6 - 4 = 4 - 2 = 2
Jika suku pertama dinyatakan dengan a, maka bentuk umum barisan aritmatika adalah :
...
bentuk di atas adalah bentuk umum dari barisan aritmatika
sehingga,
Untuk mengetahui nilai suku ke-n dari suatu barisan aritmatika dapat diketahui dengan mengetahui nilai suku pertama dan selisih antar suku yang berdekatan (b).
Deret Aritmatika adalah penjumlahan dari suku-suku anggota barisan aritmatika. Jumlah n suku pertama deret aritmatika disimbolkan dengan
atau
atau
Persamaan di atas bisa kita gunakan juga untuk mencari nilai suku ke-n, kita ketahui bahwa,
dan
sehingga kedua rumus di atas memiliki hubungan yaitu :
atau
Sisipan Pada Barisan Aritmatika
Misalkan  adalah suatu barisan aritmatika dengan suku pertama
adalah suatu barisan aritmatika dengan suku pertama  , beda =
, beda =  , dan banyaknya suku =
, dan banyaknya suku =  . Apabila di antara dua suku disisipkan k buah suku (suku baru) sehingga membentuk barisan aritmatika baru, maka :
. Apabila di antara dua suku disisipkan k buah suku (suku baru) sehingga membentuk barisan aritmatika baru, maka :
barisan mula-mula : ,(a+2b),...)
barisan baru : ,(a+2b),...(a+kb),a(k-1)b,...)
karena terdapat sisipan di antara dua suku, maka diperoleh hubungan :
1. Beda baru
Keterangan :
2. banyak suku baru
Keterangan :
sehingga,
3. jumlah n suku pertama sesudah sisipan
Suku Tengah Barisan Aritmatika
-------------------------------------------------------------------------------------------------------------------------------------------
Mungkin itu saja pembahasan kali ini tentang Baris dan Deret Aritmatika yang bisa saya jabarkan, semoga saja pembahasan ini berguna bagi teman-teman semua, terutama teman-teman pada jenjang Sekolah Menengah Atas. Terima kasih sudah mengunjungi kennycandra Blog. Baca Juga : Barisan dan Deret Geometri



0 komentar:
Posting Komentar